Quantifying differential rhythmicity between conditions
Source:vignettes/differential-rhythmicity.Rmd
differential-rhythmicity.RmdIntroduction
Here we show how to use limorhyde2 to quantify rhythmicity and differential rhythmicity in data from multiple conditions. The data are based on liver samples from wild-type and Rev-erb\(\alpha/\beta\) double-knockout mice (Cho et al. 2012 and GSE34018).
Load packages
library('data.table')
library('ggplot2')
library('limorhyde2')
library('qs')
# doParallel::registerDoParallel() # register a parallel backend to minimize runtime
theme_set(theme_bw())Load the data
The expression data are in a matrix with one row per gene and one column per sample. The metadata are in a table with one row per sample. To save time and space, the expression data include only a subset of genes.
y = qread(system.file('extdata', 'GSE34018_data.qs', package = 'limorhyde2'))
y[1:5, 1:5]
#> GSM840516 GSM840517 GSM840518 GSM840519 GSM840520
#> 12686 11.962830 11.923338 11.098814 10.958933 9.256413
#> 13170 8.989743 9.132606 12.381036 12.441759 14.766070
#> 26897 11.515292 11.625519 10.579969 10.601969 11.096489
#> 11287 7.985859 7.930935 7.674688 7.899531 7.768563
#> 11731 8.481372 8.114623 8.058194 8.144267 8.152959
metadata = qread(system.file('extdata', 'GSE34018_metadata.qs', package = 'limorhyde2'))
metadata
#> sample cond time
#> 1: GSM840516 wild-type 0
#> 2: GSM840517 wild-type 0
#> 3: GSM840518 wild-type 4
#> 4: GSM840519 wild-type 4
#> 5: GSM840520 wild-type 8
#> 6: GSM840521 wild-type 8
#> 7: GSM840522 wild-type 12
#> 8: GSM840523 wild-type 12
#> 9: GSM840524 wild-type 16
#> 10: GSM840525 wild-type 16
#> 11: GSM840526 wild-type 20
#> 12: GSM840527 wild-type 20
#> 13: GSM840504 knockout 0
#> 14: GSM840505 knockout 0
#> 15: GSM840506 knockout 4
#> 16: GSM840507 knockout 4
#> 17: GSM840508 knockout 8
#> 18: GSM840509 knockout 8
#> 19: GSM840510 knockout 12
#> 20: GSM840511 knockout 12
#> 21: GSM840512 knockout 16
#> 22: GSM840513 knockout 16
#> 23: GSM840514 knockout 20
#> 24: GSM840515 knockout 20
#> sample cond timeFit linear models and compute posterior fits
Because the samples were acquired at relatively low temporal resolution (every 4 h), we use three knots instead of the default four, which reduces the flexibility of the spline curves. We specify condColname so getModelFit() knows to fit a differential rhythmicity model.
fit = getModelFit(y, metadata, nKnots = 3L, condColname = 'cond')
fit = getPosteriorFit(fit)
#> - Computing 100 x 109 likelihood matrix.
#> - Likelihood calculations took 0.09 seconds.
#> - Fitting model with 109 mixture components.
#> - Model fitting took 0.03 seconds.
#> - Computing posterior matrices.
#> - Computation allocated took 0.02 seconds.Get rhythmic statistics
Next, we use the posterior fits to compute rhythmic statistics for each gene in each condition.
rhyStats = getRhythmStats(fit)
print(rhyStats, nrows = 10L)
#> cond feature peak_phase peak_value trough_phase trough_value
#> 1: wild-type 12686 23.583282 11.844107 10.4736761 8.785513
#> 2: wild-type 13170 9.444423 15.019936 22.2707495 9.113807
#> 3: wild-type 26897 18.166330 12.367458 4.7795034 10.697741
#> 4: wild-type 11287 21.613506 7.921370 7.5466856 7.778185
#> 5: wild-type 11731 16.271138 8.251227 4.8812985 8.207653
#> ---
#> 196: knockout 382038 17.994402 8.122326 0.4356467 8.030396
#> 197: knockout 404323 6.101673 8.070874 23.1863197 8.063530
#> 198: knockout 435684 10.576267 8.292289 19.1186125 8.287769
#> 199: knockout 622408 6.101719 7.927632 23.6722205 7.902385
#> 200: knockout 110599566 21.559365 8.922764 12.6101340 8.909615
#> peak_trough_amp rms_amp mean_value
#> 1: 3.058593622 1.073445705 10.368427
#> 2: 5.906128877 2.078735725 12.018767
#> 3: 1.669716330 0.594546001 11.675870
#> 4: 0.143185025 0.049291689 7.854743
#> 5: 0.043574326 0.015641890 8.233332
#> ---
#> 196: 0.091930147 0.027487564 8.072759
#> 197: 0.007343261 0.002194299 8.067516
#> 198: 0.004520197 0.001443692 8.290186
#> 199: 0.025246670 0.007586063 7.916088
#> 200: 0.013148403 0.004548861 8.917391Get differentially rhythmic statistics
We can now calculate the rhythmic differences for each gene between any two conditions, here between wild-type and knockout.
diffRhyStats = getDiffRhythmStats(fit, rhyStats)
print(diffRhyStats, nrows = 10L)
#> feature cond1 cond2 diff_mean_value diff_peak_trough_amp
#> 1: 101476 wild-type knockout 0.385079194 -0.119024736
#> 2: 104662 wild-type knockout -0.088926109 -0.120641471
#> 3: 107652 wild-type knockout 0.030761445 -0.343503780
#> 4: 109359 wild-type knockout 0.009406463 -0.039640031
#> 5: 110599566 wild-type knockout -0.006050343 -0.057446071
#> ---
#> 96: 76629 wild-type knockout -0.045727952 -0.025321758
#> 97: 78174 wild-type knockout 0.003833334 -0.002883578
#> 98: 80782 wild-type knockout 0.019076587 -0.026706196
#> 99: 93671 wild-type knockout -0.122202398 0.318458377
#> 100: 97064 wild-type knockout -0.066047812 -0.057648476
#> diff_rms_amp diff_peak_phase diff_trough_phase rms_diff_rhy
#> 1: -0.050009025 -1.5431221 -3.6419347 0.231750686
#> 2: -0.048870179 7.5438911 5.1482949 0.201688499
#> 3: -0.115274715 -2.3486873 -4.2596862 0.390392048
#> 4: -0.014145087 -0.7842197 -3.2539909 0.045821389
#> 5: -0.019823612 8.0133286 7.9850954 0.079889026
#> ---
#> 96: -0.009408998 6.4503647 8.6171045 0.041815280
#> 97: -0.001211714 1.6270477 -2.0338405 0.004473018
#> 98: -0.009274696 0.1900240 -0.4066909 0.028202979
#> 99: 0.102493077 -3.5169301 11.3633377 1.044134449
#> 100: -0.020596285 -2.0915970 -7.9439872 0.068376386We can examine the distributions of the statistics in various ways, such as ranking genes by difference in peak-to-trough amplitude (no p-values necessary) or plotting difference in peak-to-trough amplitude vs. difference in mean expression.
print(diffRhyStats[order(diff_peak_trough_amp)], nrows = 10L)
#> feature cond1 cond2 diff_mean_value diff_peak_trough_amp
#> 1: 13170 wild-type knockout 1.200806055 -3.533865155
#> 2: 12686 wild-type knockout -0.414207921 -2.406530463
#> 3: 26897 wild-type knockout -2.388261031 -1.034124834
#> 4: 20211 wild-type knockout -1.131052863 -0.699250756
#> 5: 12977 wild-type knockout -0.027363903 -0.473937425
#> ---
#> 96: 329910 wild-type knockout -0.084197747 0.003591791
#> 97: 20497 wild-type knockout 0.023894611 0.004206791
#> 98: 58229 wild-type knockout -0.005650829 0.004711548
#> 99: 18378 wild-type knockout -0.059531404 0.088706917
#> 100: 93671 wild-type knockout -0.122202398 0.318458377
#> diff_rms_amp diff_peak_phase diff_trough_phase rms_diff_rhy
#> 1: -1.2402582569 -0.9555117 -0.5424612 3.802135940
#> 2: -0.8550873280 -4.9265939 -1.1261574 2.828991912
#> 3: -0.3915656446 0.7545927 6.2343634 1.479902146
#> 4: -0.2563897925 -2.7175892 -10.1197405 1.241164124
#> 5: -0.1682833503 -1.3111235 -4.7103687 0.521668016
#> ---
#> 96: 0.0031446455 9.0552937 9.5536510 0.197597118
#> 97: 0.0008941407 8.1356528 8.3626192 0.018547619
#> 98: 0.0013749504 10.9831840 -3.2542325 0.007650559
#> 99: 0.0237101323 9.3201219 8.6090161 0.256049333
#> 100: 0.1024930767 -3.5169301 11.3633377 1.044134449
ggplot(diffRhyStats) +
geom_point(aes(x = diff_mean_value, y = diff_peak_trough_amp), alpha = 0.2) +
labs(x = 'Difference in mean expression (norm.)',
y = 'Difference in peak-to-trough amplitude (norm.)')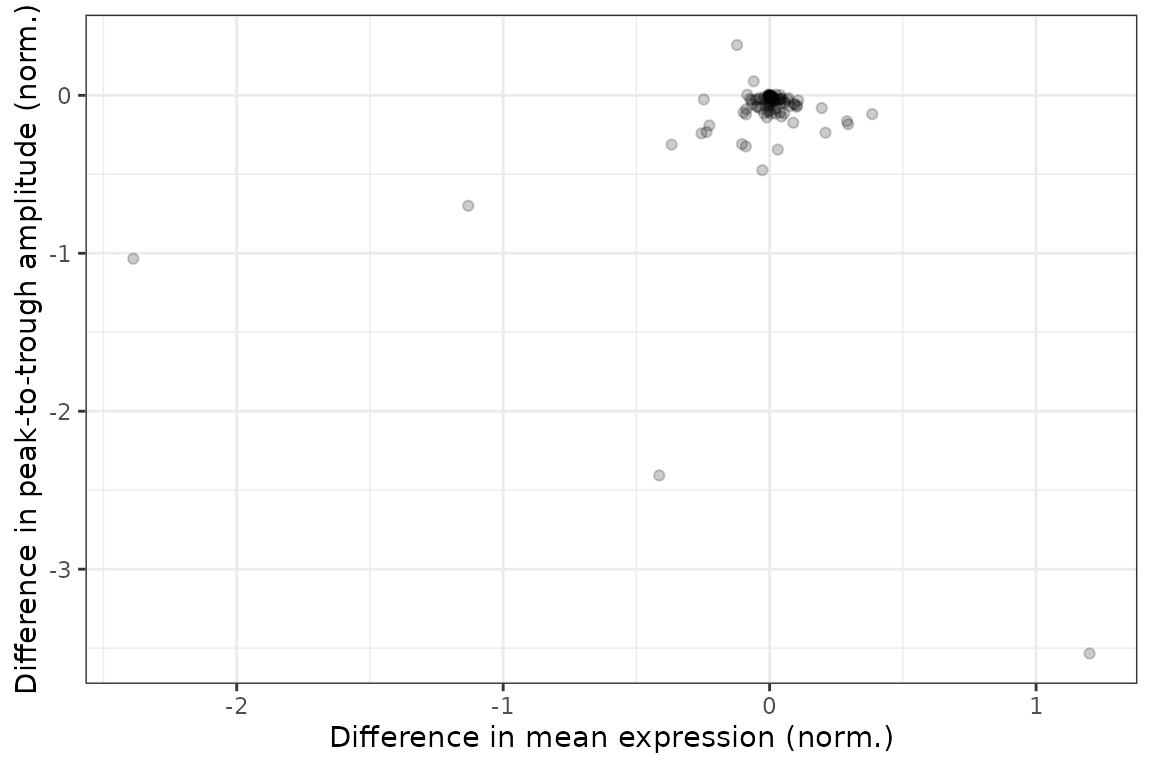
Get observed and fitted time-courses
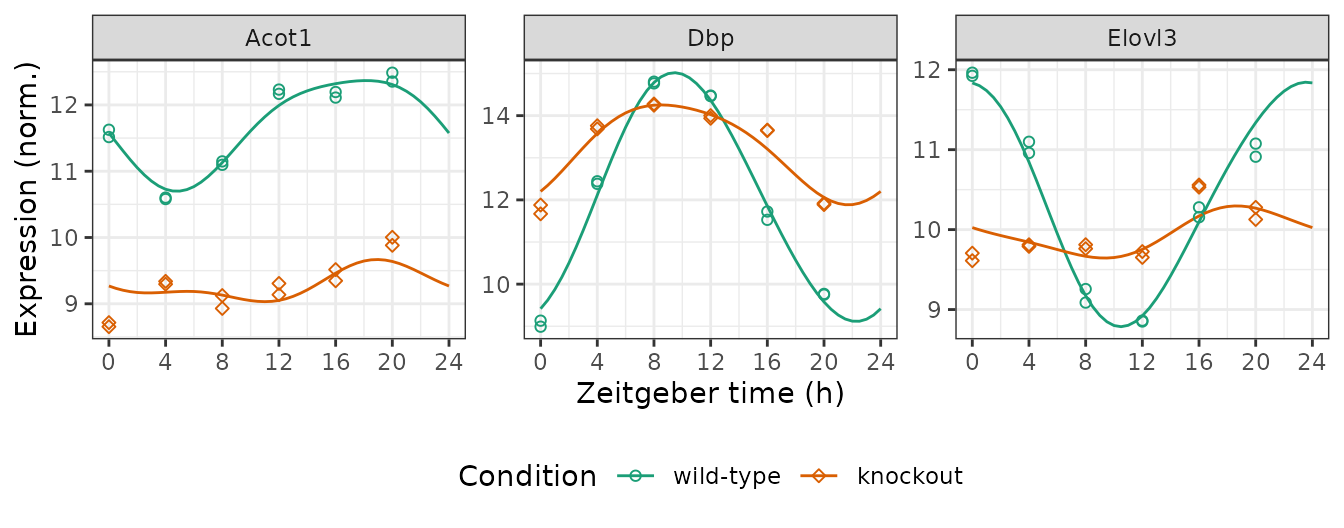
We can compute the expected measurements for one or more genes at one or more time-points in each condition, which correspond to the fitted curves. Here we plot the posterior fits and observed expression for three genes (converting from gene id to gene symbol).
genes = data.table(id = c('13170', '12686', '26897'),
symbol = c('Dbp', 'Elovl3', 'Acot1'))
measFit = getExpectedMeas(fit, times = seq(0, 24, 0.5), features = genes$id)
measFit[genes, symbol := i.symbol, on = .(feature = id)]
print(measFit, nrows = 10L)
#> time cond feature value symbol
#> 1: 0 wild-type 13170 9.416439 Dbp
#> 2: 0 wild-type 12686 11.835367 Elovl3
#> 3: 0 wild-type 26897 11.575952 Acot1
#> 4: 0 knockout 13170 12.200770 Dbp
#> 5: 0 knockout 12686 10.025091 Elovl3
#> ---
#> 290: 24 wild-type 12686 11.835367 Elovl3
#> 291: 24 wild-type 26897 11.575952 Acot1
#> 292: 24 knockout 13170 12.200770 Dbp
#> 293: 24 knockout 12686 10.025091 Elovl3
#> 294: 24 knockout 26897 9.268390 Acot1Next we combine the observed expression data and metadata. The curves show how limorhyde2 is able to fit non-sinusoidal rhythms.
measObs = mergeMeasMeta(y, metadata, features = genes$id)
measObs[genes, symbol := i.symbol, on = .(feature = id)]
print(measObs, nrows = 10L)
#> sample cond time feature meas symbol
#> 1: GSM840504 knockout 0 13170 11.669138 Dbp
#> 2: GSM840504 knockout 0 12686 9.705361 Elovl3
#> 3: GSM840504 knockout 0 26897 8.654624 Acot1
#> 4: GSM840505 knockout 0 13170 11.877697 Dbp
#> 5: GSM840505 knockout 0 12686 9.611530 Elovl3
#> ---
#> 68: GSM840526 wild-type 20 12686 10.911935 Elovl3
#> 69: GSM840526 wild-type 20 26897 12.486105 Acot1
#> 70: GSM840527 wild-type 20 13170 9.749365 Dbp
#> 71: GSM840527 wild-type 20 12686 11.075636 Elovl3
#> 72: GSM840527 wild-type 20 26897 12.352601 Acot1
ggplot() +
facet_wrap(vars(symbol), scales = 'free_y', nrow = 1) +
geom_line(aes(x = time, y = value, color = cond), data = measFit) +
geom_point(aes(x = time %% 24, y = meas, color = cond, shape = cond),
size = 1.5, data = measObs) +
labs(x = 'Zeitgeber time (h)', y = 'Expression (norm.)',
color = 'Condition', shape = 'Condition') +
scale_x_continuous(breaks = seq(0, 24, 4)) +
scale_color_brewer(palette = 'Dark2') +
scale_shape_manual(values = c(21, 23)) +
theme(legend.position = 'bottom')